Cone
Ao estudarmos Geometria
nos deparamos com várias situações geométricas, alguns sólidos possuem origem e
fundamentos na sua formação, um deles é o cone, figura presente no cotidiano. Dado
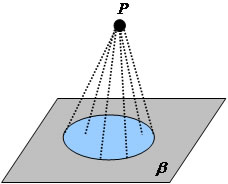
um círculo de centro O e raio R no plano B, e um ponto P fora do plano. O cone
será formado por segmentos de reta unindo o ponto P aos pontos do círculo.
Outra forma de construir o cone é através da revolução do triângulo retângulo sobre um eixo vertical.
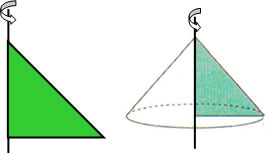
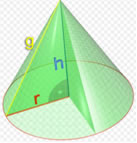
g: geratriz do cone
h: altura do cone
r: raio da base
v: vértice
Classificação do Cone
No
cone reto podemos aplicar a relação de Pitágoras para o cálculo da geratriz
(g), do raio da base (r) e da altura (h), pois vimos que o cone pode ser
formado através da revolução do triângulo retângulo. Comparando os elementos do
cone aos do triângulo retângulo temos:
Geratriz no cone, hipotenusa no triangulo.
Altura no cone, cateto no trinagulo.
Raio da base no cone, cateto no triângulo.
Uma importante relação no cone é dada por: r² + h² = g², observe a figura:
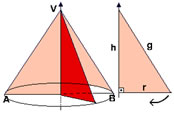
Áreas no cone
Área da base
Por ser uma circunferência, a área da base de um cone é dada pela seguinte expressão:
Área da lateral
A área lateral do cone é dada pela seguinte expressão:Área total
É dada somando-se a área lateral e a área da base.
At = Al + Ab
Volume do cone
O volume do cone é dado pelo produto da área da base pela altura divido por três.
V = (Πr²h)/3

Ângulo Central
A= piR/G (radianos)
A= 360.R/G (graus)
O sector circular obtido tem um arco igual ao
perímetro da base do cone , ou seja , 2πR .
O sector faz parte de um círculo de raio G , que portanto tem perímetro 2πG .
Então basta uma regra de 3 : se o perímetro total 2πG tem um ângulo central de
2π radianos , então a um arco de 2πR corresponde um ângulo central de x
radianos.
2πG --------- 2π rad
2πR --------- x rad
x = 2πR . 2π / 2πG
x = 2πR/G radianos
(ou , se preferires em graus , 360R/G )
O sector faz parte de um círculo de raio G , que portanto tem perímetro 2πG .
Então basta uma regra de 3 : se o perímetro total 2πG tem um ângulo central de 2π radianos , então a um arco de 2πR corresponde um ângulo central de x radianos.
2πG --------- 2π rad
2πR --------- x rad
x = 2πR . 2π / 2πG
x = 2πR/G radianos
(ou , se preferires em graus , 360R/G )
Cone Equilatero
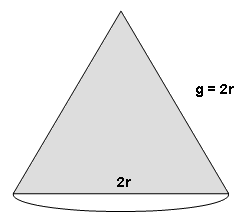
Cone equilátero
Cone eqüilátero é um cone circular reto, do qual a secção meridiana é um triângulo que denominamos cone eqüilátero. Observe:

Nenhum comentário:
Postar um comentário