Exercicios De Numeros Complexos.

 1)

 




 












2)

 
Resposta:

 
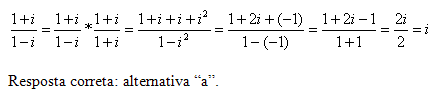
3)

 

Resposta:

 

4)

 

Resposta:

 

5)

 

Resposta:

 

6)

 

Resposta:

 

 Outros Exercícios

1) Sendo z = (m² - 5m + 6) + (m² - 1) i , determine m de modo que z seja um imaginário puro.

Solução: Para que o complexo z seja um imaginário puro, sua parte real deve ser nula ou seja, devemos ter
m² - 5m + 6 = 0, que resolvida encontramos m=2 ou m=3.

2) Determine a parte real do número complexo z = (1 + i)¹² .

Solução: Observe que (1 + i)¹² = [(1 + i)²]⁶ . Nestas condições, vamos desenvolver o produto notável 
(1 + i)² = 1² + 2.i + i² = 1 + 2i -1 = 2i \ (1 + i)² = 2i (isto é uma propriedade importante, que vale a pena ser memorizada). 

Substituindo na expressão dada, vem: 

(1 + i)¹² = [(1 + i)²]⁶ = (2i)⁶ = 2⁶.i⁶ = 64.(i²)³ = 64.(-1)³ = - 64. 
Portanto, o número complexo dado fica z = - 64 = - 64 + 0i e portanto sua parte real é igual a-64.

3) Determine a parte imaginária do número complexo z = (1 - i)²⁰⁰ .

Solução: Podemos escrever o complexo z como: z = [(1 - i)²]¹⁰⁰ . Desenvolvendo o produto notável 
(1 - i)² = 1² - 2.i + i² = 1 - 2i -1 = - 2i \ (1 - i)² = - 2i (isto é uma propriedade importante, que merece ser memorizada). 

Substituindo na expressão dada, vem: 

z = (- 2i)¹⁰⁰ = (- 2)¹⁰⁰. i¹⁰⁰ = 2¹⁰⁰ . i¹⁰⁰ = 2¹⁰⁰ . ( i² )⁵⁰ = 2¹⁰⁰. (- 1)⁵⁰ = 2¹⁰⁰ . 1 = 2¹⁰⁰. 
Logo, o número complexo z é igual a 2¹⁰⁰ e portanto um número real. Daí concluímos que a sua parte imaginária é zero.