Geometria Plana
A geometria plana, também chamada de geometria elementar ou Euclidiana,
teve inicio na Grécia antiga. Esse estudo analisava as diferentes formas de
objetos, e baseia-se em três conceitos básicos: ponto, reta e plano.
Ponto: Não tem definição.
Segmento de Reta: Possui INÍCIO e FIM.
Semi-Reta: Tem INÍCIO e não tem FIM.
Reta: Não tem INÍCIO e nem FIM.
Angulo
Representações:
Ô,
AÔB, BÔA ou uma letra grega.
A unidade usada para medir ângulos é o
GRAU que possui dois submúltiplos: minuto e
segundo.
1º
= 60’
Entretanto pode-se completar a definição
de ângulo, dizendo-se que ângulo é nulo (0 graus) quando seus lados coincidem e raso
(180 graus) quando seus lados são semi-retas opostas.
2- Bissetriz
É a semi-reta com origem no vértice do
ângulo e que o divide em dois ângulos iguais.
3- Classificação
a) Reto
Quando mede 90º
b) Agudo
Quando sua medida está entre 0º e 90º.
c) Obtuso
Quando
sua medida está entre 90º e 180º
4- Ângulos
opostos pelo vértice (O.P.V)
Dois ângulos são opostos pelo vértice
quando os lados de um são semi-retas opostas aos lados do outro.
5- Ângulos
complementares e ângulos suplementares
a) Ângulos
complementares
Dois ângulos são complementares quando a
soma de suas medidas é igual a 90º - Ex.: 30º e 60º
b) Ângulos
suplementares
Dois ângulos são suplementares quando a
soma de suas medidas é igual a 180º - Ex.: 60º e 120º
Poliedros
Definição:
Denomina-se poliedro o sólido limitado por polígonos planos, de modo que:
- dois desses polígonos não estão num mesmo plano;
- cada lado de um polígono é comum a dois somente dois polígonos.
Os polígonos são denominados faces do poliedro. os lados e os vértices dos polígonos denominam-se respectivamente, arestas e vértices do poliedro.
Um poliedro se diz convexo se, em relação a qualquer uma de suas faces, está todo num mesmo semiespaço determinado pelo plano que contém essa face. Caso ao contrário o poliedro e dito não convexo.
Observe um exemplo de poliedro não convexo.
De acordo com os números de faces, os poliedros convexos possuem nomes especiais.
Poliedros Regulares.
são sólidos cujas faces são polígonos regulares e geometricamente iguais.
Platão (sábio grego que viveu por volta dos 400 anos a.C) foi quem estudou os polígonos regulares e por isso são designados sólidos de Platão e estavam relacionados na Grécia Antiga às forças da Natureza.
V – A + F = 2
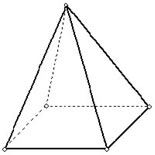
Visivelmente podemos afirmar que a pirâmide possui 5 vértices, 5 faces e 8 arestas. Vamos agora demonstrar que a relação de Euler é válida na determinação dos elementos da pirâmide de base quadrangular.
Vértices Arestas Faces
V – A + F = 2 V – A + F = 2 V – A + F = 2
V – 8 + 5 = 2 5 – A + 5 = 2 5 – 8 + F = 2
V = 2 + 3 –A = 2 – 1 0–3 + F = 2
V = 5 –A = –8 x(–1) F = 2 + 3
Relação de Euler
Em todo poliedro convexo vale a relação:
A + 2 = V + F ou V - A + F = 2
Em que:
- V: número de vértices
- A: número de arestas
- F: números de faces
Exemplos:
Determine o número de faces de um sólido que possui 10 arestas e 6 vértices.
Resolução:
V – A + F = 2
6 – 10 + F = 2
–4 + F = 2
F = 4 + 2
F = 6
Portanto, o sólido possui 6 faces.
Exemplo 2 :
Determine o número de vértices da pirâmide quadrangular a seguir:

Visivelmente podemos afirmar que a pirâmide possui 5 vértices, 5 faces e 8 arestas. Vamos agora demonstrar que a relação de Euler é válida na determinação dos elementos da pirâmide de base quadrangular.
Resolução:
Vértices Arestas Faces
V – A + F = 2 V – A + F = 2 V – A + F = 2
V – 8 + 5 = 2 5 – A + 5 = 2 5 – 8 + F = 2
V = 2 + 3 –A = 2 – 1 0–3 + F = 2
V = 5 –A = –8 x(–1) F = 2 + 3
A = 8 F = 5
c) Paralelogramo
d) Losango
e) Trapézio
2- Triângulos
a) Sendo dadas: base e
altura
b) Sendo dados: os três lados
c) Triângulo equilátero
d) Triângulo retângulo
Assista ao Vídeo para melhor aprendizagem do conteúdo.













.jpg)











